Kerékparadoxon: amikor az elméletileg lehetetlen simán megvalósul a valóságban

Az élet tele van paradoxonokkal, amikre sokszor rá se hederítünk. Néha az elmélet egyszerűen nem egyezik a gyakorlattal. Íme egy példa.

Képzelj el egy autógumit. Van a felni, amire a gumiabroncsot szerelték. A felni és a gumiabroncs, most már egy egységet alkotva – a kerék – szinkronban gördül, csúszás nélkül. A paradoxon az, hogy a felni és a gumiabroncsnak más a sugara, és emiatt más a kerületük is, de mégis ugyanazt a távot teszik meg. Hogy lehet ez?

Ezt a mechanikai-matematikai paradoxont már az ókorban is észrevették, de először Arisztotelész írta le és tanulmányozta a „Mechanika” című művében. Ezért a kerék paradoxonát Arisztotelész kerekének is nevezik. Később Galileo Galilei is foglalkozott ezzel a paradoxonnal, de végül a francia Jean Jacques de Meran magyarázta meg 1715-ben.

Teljesen egyértelmű, hogy ha fogunk egy felnit és végiggurítjuk a homokon, hogy teljes fordulatot tegyen, majd fogjuk a gumiabroncsot és ugyanígy végiggurítjuk mellette egy teljes fordulatot, akkor a gumiabroncs nyoma hosszabb lesz. De miért tesznek meg ugyanazt a távot, ha a gumiabroncs a felnire van szerelve?

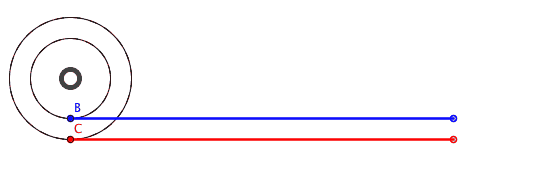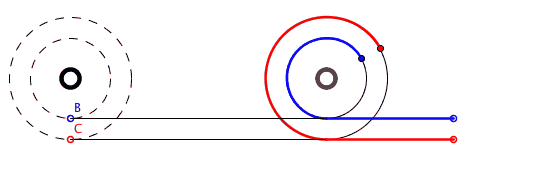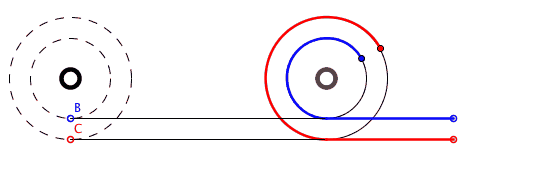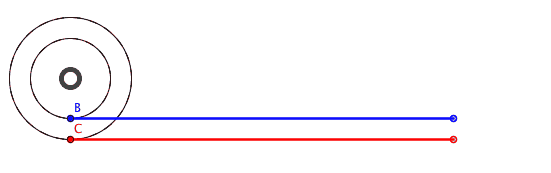
A fenti animáció szemléletesen mutatja, hogy az A és B pontok által megtett utak (kék és piros színnel jelölve) egyenlőek. Azonban ez elsőre lehetetlennek tűnik, hiszen a kerület hossza 2rπ, és a felni sugara kisebb, mint a gumiabroncs külső sugara. A kék útnak rövidebbnek kellene lennie! Ellenkező esetben azt is állíthatnánk, hogy egy 5 cm kerületű kerék ugyanazt a távolságot tudja megtenni egy fordulat alatt, mint egy 5 méter kerületű kerék!

Ez azonban sem a gyakorlatban, sem az elméletben nem lehetséges. Tehát mi a helyzet?

Ahhoz, hogy megértsük, mi történik valójában, meg kell vizsgálnunk a két kiválasztott pont, a felni peremén és a gumiabroncs külső sugarán lévő pontok mozgáspályáját.

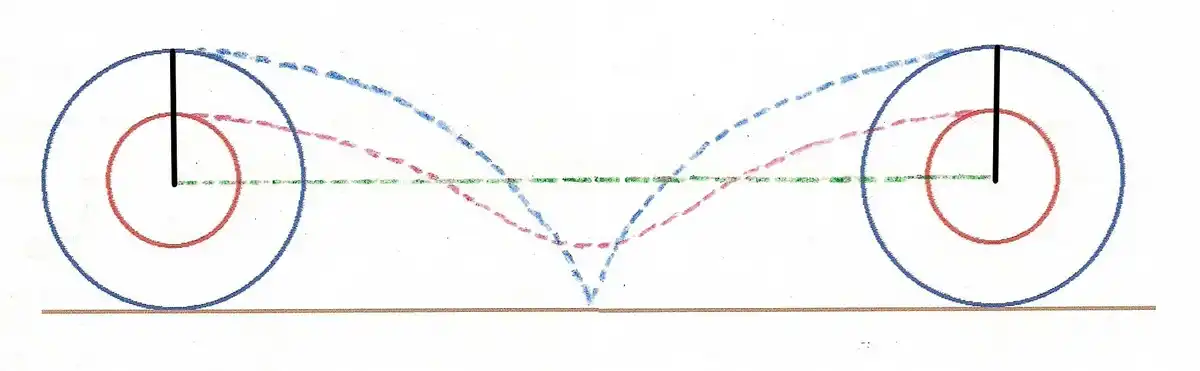
A pályákat (kék és piros), amiket a pontok leírnak, cikloisnak nevezzük. Könnyen észrevehető, hogy ezeknek a pályáknak a hossza nem azonos. A kék hosszabb, mint a piros.

És minél kisebb a kerék felnijének sugara, annál jobban kiegyenesedik a piros ciklois, a zöld egyenes felé törekedve.

Tehát valójában itt nincs paradoxon. Csak a „pálya” és az „elmozdulás” fogalmai között van egy kis keveredés. A két pont elmozdulása valóban azonos, de a megtett út nem.

Elmozdulás: a pont kiinduló és véghelyzetét összekötő irányított egyenes.

Pálya: a pont által megtett út hossza (az a vonal, amely mentén a pont mozog).

Képzeld el, hogy Budapestről Debrecenbe utazol. Mehetsz Miskolc és Nyíregyháza érintésével, de Szolnok, Kecskemét és Berettyóújfalu érintésével is. A távolság (elmozdulás) Budapest és Debrecen között azonos lesz, de a megtett út eltérő. A kerék paradoxona pontosan ezen alapul.