Egyelőre azt javaslom, gondolkodj el rajta önállóan. Előtted egy négyzet látható, amit négy négyszögre osztottak. Ezek közül háromnak ismert a területe, a negyedikét pedig neked kell megtalálnod. A négyzet területe nem ismert, azt viszont tudjuk, hogy a nagy négyzet oldalait a belső négyszögek oldalai felezik. Röviden: minden itt van a rajzon.
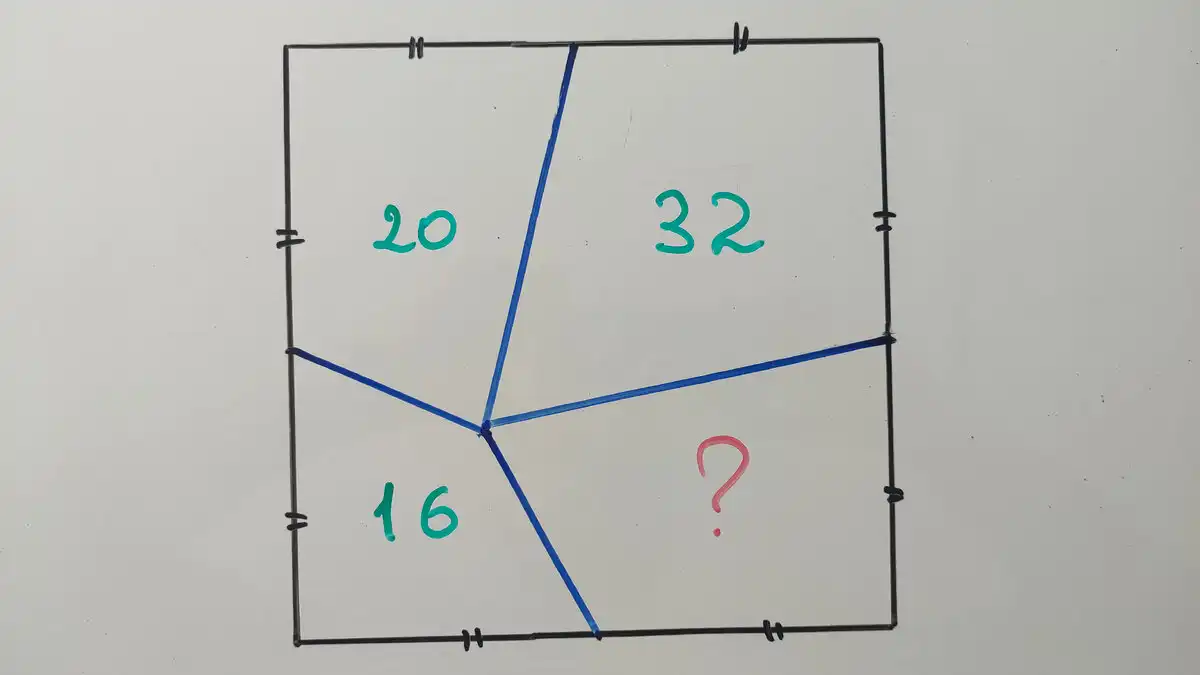
Mit szólsz hozzá? Hogyan oldanád meg? Valószínűleg a legnépszerűbb feltételezés az, hogy az ismeretlen terület 28. De hogyan jutsz el ehhez az eredményhez? Használhatod azt az állítást, hogy ha a (nagy) négyzet oldalai felezve vannak (ahogy a mi esetünkben is), akkor érvényes az S1+S3=S2+S4 összefüggés. Vagyis két, átlósan elhelyezkedő alakzat területének összege egyenlő a másik két alakzat területének összegével.
A mi esetünkben a keresett S terület 16+32−20=28. Úgy tűnik, az eredmény helyes. De van egy fontos apróság. Nem bizonyítottuk azt az állítást, amelyre támaszkodtunk. Pedig illett volna. Én ezt most nem teszem meg, de te próbáld meg először is áthelyezni a négyszögek közös belső pontját a nagy négyzet középpontjába. Így négy egybevágó kisnégyzetet kapsz, melyek oldalhossza fele a nagy négyzetének. Ebben az esetben az állítás nyilvánvaló. Aztán mozgasd ezt a belső pontot, és igazold az állítást a pont tetszőleges helyzetére és az így keletkező általános (nem feltétlenül szabályos) négyszögekre is.
Én viszont elmondok egy olyan megoldási módszert, ami az eleganciája miatt tetszett meg nekem. Itt nincs szükség semmiféle bizonyításra. Egyszerűen csak hetedikes képleteket és ismereteket használunk. Ez valószínűleg nem a leggyorsabb, cserébe viszont egyszerű. Ha vannak ennél eredetibb ötleteid, oszd meg őket kommentben!
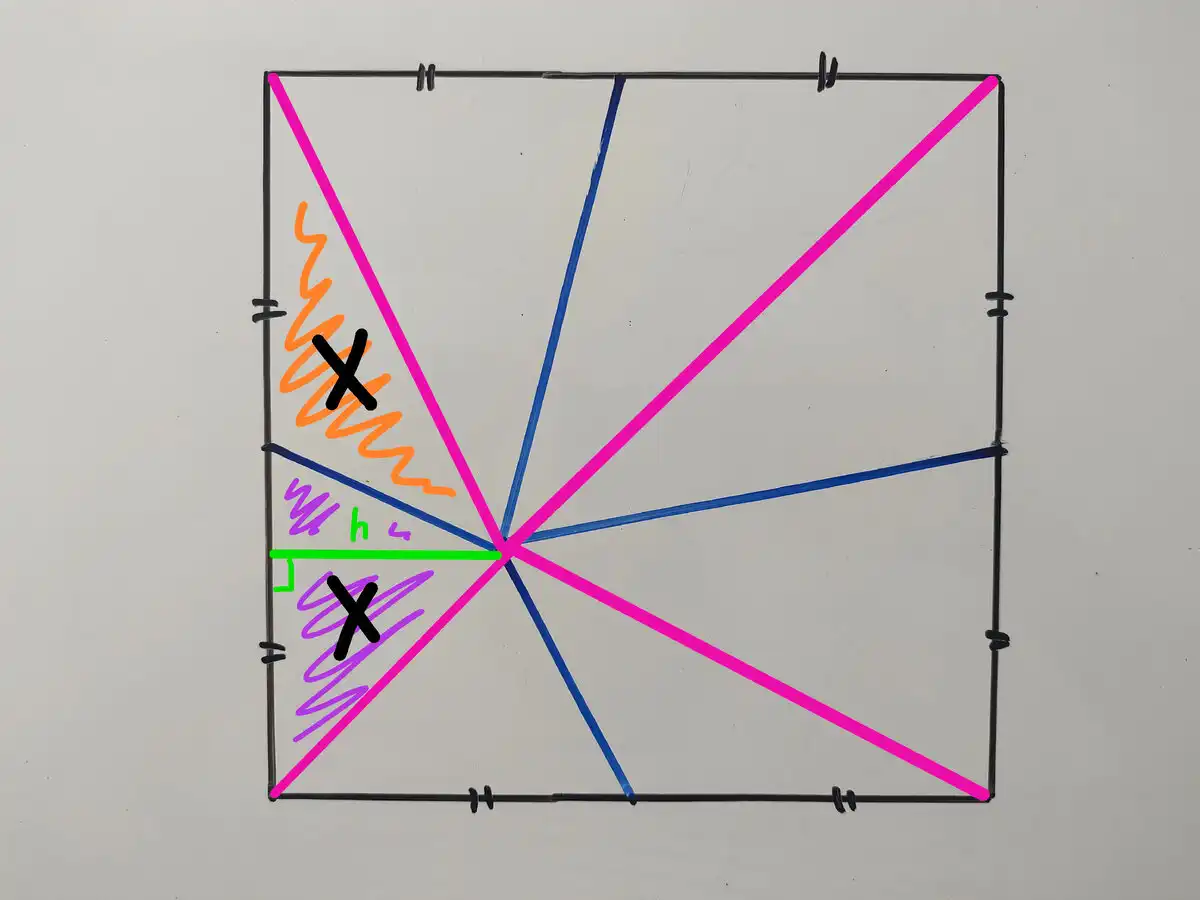
Osszuk fel mindegyik négyszöget az átlójával két részre! És vizsgáljunk meg két háromszöget (narancssárgával és lilával satírozva), melyek területe egyenlő, mivel azonos a magasságuk (a h magasságot halványzölddel jelöltük az ábrán), és az alapjuk is egyenlő (mégpedig a nagy négyzet oldalának a fele). Jelöljük ezen háromszögek területét X-szel.
Ezekből az X-ekből indulunk ki. Az 1. számú háromszög (lásd az alábbi ábrát) területe (20−X), és ez megegyezik a 2. számú háromszög területével (azonos magasság és egyenlő alapok miatt). Mivel a 2-es és 3-as sorszámú háromszögekből álló négyszög területe 32, ebből következik, hogy a 3-as sorszámú háromszög területe 32−(20−X)=12+X. Mivel a 3-as és 4-es háromszögnek is azonos a magassága és egyenlő az alapja, így a 4-es számú háromszög területe szintén 12+X.
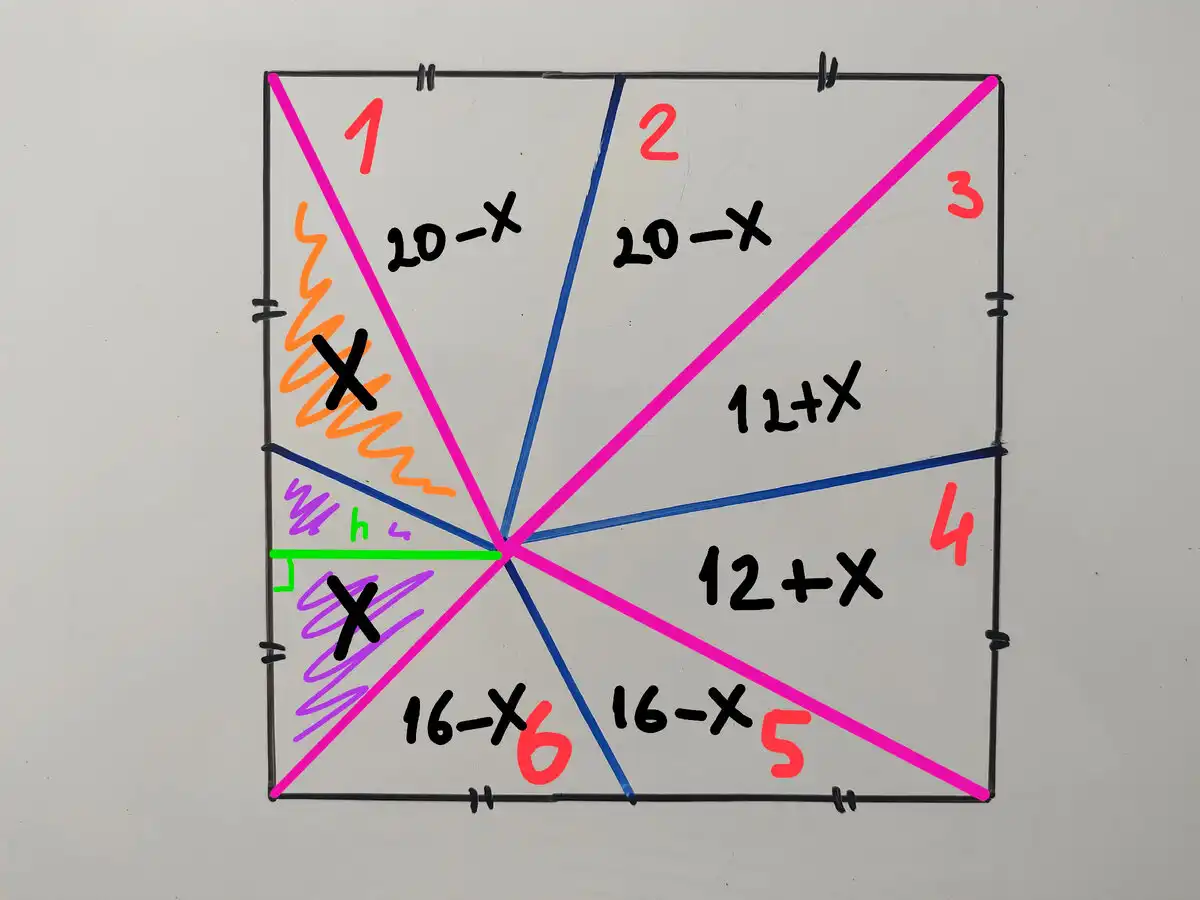
Most térjünk át a 6. számú háromszögre. Ennek területe megegyezik az 5. számú háromszög területével (ismét azonos magasság és egyenlő alapok miatt). Mivel pedig a 6. számú háromszög területe (16−X), így az 5. számú háromszög területe is (16−X).
Most már láthatod, hogy a keresett négyszög a 4-es és 5-ös sorszámú háromszögekből áll. Ha összeadjuk a területeiket, ezt kapjuk: (12+X) + (16−X) = 28. Ahogy láthatod, az eredmény ugyanaz, de ez a megoldás kizárólag a háromszögek területén alapult. Semmi szükség nem volt bonyolult tételekre vagy bizonyításokra.
Na, hogy tetszett a feladat? Engem ez a fejtörő nagyon megfogott. Éppen azért, mert bármelyik hetedikes meg tudja oldani.
A BEJEGYZÉS A HIRDETÉS ALATTI GOMBBAL FOLYTATÓDIK


























